TEOREMA DE PICK: auxílio no ensino de geometria

Francisco Silverio da Silva Junior
Licenciado em Matemática e Mestre profissional (PROFMAT) pela Universidade Federal de Alagoas. Foi professor de Educação Básica da rede municipal de ensino de Rio Largo-AL e professor do Curso Superior de Engenharia Civil do CESMAC. Atualmente é professor de ensino técnico integrado de nível médio no Instituto Federal de Alagoas.
E-mail: francisconada@hotmail.com

Fernando Valério Ferreira de Brito
Licenciado em Matemática e Mestre profissional (PROFMAT) pela Universidade Federal de Alagoas. Foi professor de Educação Básica da rede estadual de ensino de Alagoas e atualmente é professor de ensino técnico integrado de nível médio no Instituto Federal de Alagoas.
E-mail: fernandobrito500@gmail.com

Tiago Marinho da Silva
Professor de Matemática formado pela Universidade Federal da Alagoas. Foi professor da rede estadual de educação de Alagoas e atualmente é professor do Instituto Federal de Alagoas.
E-mail: tiaggomatt@hotmail.com

Alina Lara Souza Cruz
Antiga aluna do curso técnico em Meio Ambiente no Instituto Federal de Educação, Ciência e Tecnologia de Alagoas (IFAL)- Câmpus Penedo. Atualmente, faz curso técnico em Química no Instituto Federal de Educação, Ciência e Tecnologia de Alagoas (IFAL)- Câmpus Maceió
E-mail: alinalarasc@hotmail.com

Vyda Nery Alves
Estudante do 4º ano do curso técnico de Meio Ambiente integrado ao ensino médio pelo IFAL – Campus Penedo. Entre os anos de 2016 e 2017 participou dos projetos de pesquisa O Teorema de Pick, o Geoplano e o Geogebra: Uma forma de transpor as dificuldades no ensino da geometria e Os Estilos Artísticos e o Tombamento da Cidade, e do projeto de ensinoLecturas Filosoficas: La Historia y lo Cotidiano, atualmente participa do projeto de pesquisa A Publicização do Tempo do Relógio na Paisagem do Centro Histórico de Penedo (AL).
E-mail: vydanery.10@gmail.com
INTRODUÇÃO
Este artigo é o resultado do projeto de pesquisa “O Teorema de Pick, o geoplano e o geogebra: Uma forma de transpor as dificuldades no ensino de geometria”, que foi realizado no Instituto Federal de Alagoas, campus Penedo – AL, entre agosto de 2016 e julho de 2017.
O projeto foi pensado como uma tentativa de diminuir os altos índices de evasão e repetência no campus onde foi realizado e acreditamos que muito desse fenômeno se deva às dificuldades em Matemática e, mais ainda, em Geometria, que geralmente é tratada com certo descaso em comparação aos conteúdos algébricos e aritméticos. Isso porque muitos professores não se sentem preparados para lecionar Geometria quanto estariam para o ensino algébrico, apesar da grande importância dos conceitos geométricos por se tratar do estudo das formas tão presentes em nosso dia a dia. Como afirma (PAVANELLO, 1993, p. 16):
Existem fortes motivos para a inquietação dos professores com o abandono da geometria e sua insistência em melhorar seus conhecimentos com relação a ela. A ausência do ensino de geometria e a ênfase no da álgebra pode estar prejudicando a formação dos alunos por privá-los da possibilidade do desenvolvimento integral dos processos de pensamento necessários à resolução de problemas matemáticos. Atiyah salienta a necessidade de cultivar e desenvolver tanto o pensamento visual, dominante na geometria, quanto o sequencial, preponderante na álgebra, pois ambos são essenciais aos problemas matemáticos autênticos.
Além disso, é comum o ensino de Geometria ser realizado de forma pouco atrativa, concentrando-se, em grande parte, na memorização de fórmulas e propriedades geométricas abstratas. Isso acaba se refletindo no baixo interesse dos discentes em estudar os conteúdos geométricos, culminando, em alguns casos, em evasão ou repetência, especialmente quando parte dos estudantes já apresenta dificuldades matemáticas anteriores.
Por outro lado, com a globalização e o rápido desenvolvimento tecnológico, houve uma explosão de mídias sociais e dos chamados smartphones, que são capazes de conectar pessoas em quaisquer lugares do mundo em tempo real e hoje vemos um grande interesse dos jovens pela interatividade das mídias sociais e no manuseio dos aparelhos eletrônicos móveis.
A partir dessa reflexão, por meio de um projeto, pensamos na possibilidade de apresentar o ensino de Geometria de uma forma mais dinâmica, fazendo uso de softwares de computadores ou celulares, materiais didáticos e de uma fórmula de fácil entendimento e de grande utilidade.
Isso seria capaz de trazer para os jovens um novo significado para o ensino de Geometria, baseado na experimentação e no manuseio das formas por meio de construções em softwares e aplicativos e de atividades que tragam o real significado do estudo da Geometria e suas formas. Como afirmam os Parâmetros Curriculares Nacionais (BRASIL 1997, pp. 81-82):
É multiplicando suas experiências sobre os objetos do espaço em que vive, que a criança aprenderá a construir uma rede de conhecimentos relativos à localização, à orientação, que lhe permitirá penetrar no domínio da representação dos objetos e, assim, distanciar-se do espaço sensorial ou físico. É o aspecto experimental que colocará em relação esses dois espaços: o sensível e o geométrico. De um lado, a experimentação permite agir, antecipar, ver, explicar o que se passa no espaço sensível, e, de outro, possibilita o trabalho sobre as representações dos objetos do espaço geométrico e, assim, desprender-se da manipulação dos objetos reais para raciocinar sobre representações mentais.
Assim, acreditamos que o trabalho citado acima tenha sido capaz de trazer mais significado no processo de ensino e aprendizagem de Geometria, em especial no tratamento dos conceitos de perímetro e área de figuras planas.
O TEOREMA DE PICK
O Teorema de Pick permite o cálculo de áreas de polígonos diversos a partir da simples contagem de pontos de um plano reticulado, o que o torna uma boa alternativa, capaz de substituir o processo habitual do cálculo de áreas, principalmente em polígonos de formas mais irregulares, que não apresentam uma fórmula única para o cálculo de suas áreas.
Sendo assim, o Teorema de Pick nos diz que dado um polígono P, simples e sem autointersecção, cujos vértices são pontos de coordenadas inteiras (ou são pontos de uma malha quadriculada de lado 1), a área de P é dada por:
![]()
onde b é a quantidade de pontos de coordenadas inteiras nas arestas de P e i é a quantidade de pontos de coordenadas inteiras interiores a P. Segue um exemplo de aplicação do teorema.
Figura 1 – Polígono numa malha quadriculada
Fonte: Francisco Silverio da Silva Junior
Nesse caso, como há dezoito pontos nas arestas do polígono P (incluindo seus vértices) e cinco pontos interiores ao mesmo, segue-se que
![]()
A discussão, demonstração, sua versão para polígono com buracos e sua equivalência com a fórmula de Euler no plano são discutidos em SILVA JÚNIOR (2013).
OBJETIVOS E METODOLOGIA DO PROJETO INICIAL
O projeto executado teve como objetivo principal:
- Diminuir os atuais altos índices de evasão e repetência quando causados por deficiências no ensino de Geometria.
E para atingir tal objetivo, listamos alguns objetivos específicos:
- Apresentar um ensino de Geometria baseado na experimentação e construção prática
dos conceitos, através da utilização do Teorema de Pick, do Geoplano e do Geogebra; - Elaborar uma apostila com sequências didáticas que possa auxiliar professores de Matemática no ensino dos conceitos de cálculo de áreas e perímetros de polígonos;
Para isso, as alunas do curso técnico de “Meio Ambiente”, nível médio integrado, Vyda Nery Alves (bolsista) e Alina Lara Souza Cruz (voluntária) convidaram os discentes do campus Penedo a participar do projeto, de acordo com a voluntariedade de cada um, fazendo, inicialmente, um teste[1] com algumas questões que serviram para analisar os seus conhecimentos no entendimento dos conceitos e no cálculo de área e perímetro de figuras planas.
O teste nos mostrou que grande parte dos alunos apresentava dificuldades no entendimento dos conceitos, já que cerca de 70 % da turma não havia conseguido alcançar uma nota maior que cinco pontos num teste cuja nota máxima era setenta pontos.
A seguir, foram realizadas pelas alunas bolsista e voluntária do projeto, ao longo de dez semanas, aulas de cinquenta minutos ministradas para cerca de quarenta discentes das turmas de segundo ano dos cursos técnicos de “Açúcar e Álcool” e “Meio Ambiente”, ambas do ensino médio integrado do Campus, onde os alunos puderam estudar os conceitos de área e perímetro de figuras planas com o auxílio do Teorema de Pick, do Geogebra[2] — um software matemático gratuito para PCs ou smartphones — e do Geoplano — um material didático que se assemelha a um tabuleiro com pregos igualmente espaçados, tal qual os pontos de um plano cartesiano onde é possível fazer construções de polígonos diversos e estudar suas propriedades. O Geoplano também pode ser utilizado na sua versão digital para android.
Figura 2: Geoplano Digital
Fonte: Francisco Silverio da Silva Junior
De início, foram apresentados conceitos básicos de Geometria, como vértices, arestas, diagonais e as noções de área e perímetro de polígonos, além das fórmulas usuais para o cálculo de área dos polígonos mais conhecidos (triângulo, quadrado, trapézio, losango). Isso foi feito não só para que os alunos pudessem relembrar os conceitos já vistos, mas também para facilitar a abordagem do Teorema de Pick no cálculo de áreas de figuras planas.
Nesse momento, as dificuldades no entendimento do conceito de perímetro e área de polígonos se confirmaram. Muitos não conseguiam associar o conceito de perímetro ao “tamanho da linha de contorno da figura plana”, o que nos obrigou a empregar um pouco mais de tempo que o previsto inicialmente nas aulas sobre perímetro de figuras planas. Para isso, utilizamos o Geoplano em sua versão digital para smartphones, construindo polígonos diversos e calculando seu perímetro por meio da soma dos segmentos que compunham cada polígono. Para tal atividade, foi necessário revisar e utilizar o Teorema de Pitágoras. O tratamento do conceito de perímetro de um polígono nos exigiu um total de três aulas.
Ainda maiores foram as dificuldades no entendimento do conceito de área. Muitos alunos não sabiam o porquê de associar um número real chamado área a um determinado polígono e de onde vinham as fórmulas usuais do cálculo de área dos polígonos mais conhecidos. Isso também nos obrigou a empregar mais que o tempo inicialmente planejado para o tratamento do conceito de área, dedução das fórmulas e exemplos práticos, inclusive com a ajuda do Geoplano Digital, que além de mostrar o valor do perímetro de cada figura construída, também apresenta sua área. Esse estudo sobre o conceito e cálculo de áreas foi realizado também ao longo de três aulas.
Após serem assimilados os conceitos de área e perímetro de figuras planas, pudemos apresentar aos alunos o Teorema de Pick e vimos quão surpresos ficaram quando descobriram uma fórmula que “resumia” todas as outras fórmulas antes estudadas. A princípio, foram usados diversos exemplos de aplicação do referido teorema em polígonos que satisfaziam suas condições. Também foram apresentados polígonos com autointersecção nos quais a fórmula de Pick falha no cálculo de suas áreas.
Depois disso, dividimos a turma em grupos de 5 alunos e os convidamos a construir polígonos no Geoplano Digital, com as formas mais irregulares possíveis e que respeitassem as condições do teorema, e outros polígonos que apresentassem autointersecção (onde Pick se mostra inútil). Pedimos que os alunos calculassem suas áreas pelo Teorema de Pick, culminando numa socialização dos resultados encontrados. Nesta socialização, notamos que praticamente todos os grupos acertaram nas construções dos polígonos e cálculos de suas respectivas áreas. Essa atividade pode, inclusive, motivar o cálculo de aproximações para os valores de através de polígonos regulares que aproximem o círculo, calculando suas áreas com a fórmula de Pick e utilizando a relação
![]()
Na aula seguinte, levamos os grupos ao laboratório de informática. Cada grupo ficou com um computador. Nesses computadores, pedimos aos alunos que acessassem a página virtual do Geogebra,[3] e a aplicação Pick’s Theorem.
Na aplicação, foi solicitado aos alunos que clicassem em New Problem e que depois calculassem as áreas dos polígonos apresentados na tela com a fórmula de Pick, lápis e papel. Para testar se o resultado estava correto, os alunos clicavam em Show área enclosed, quando o aplicativo mostrava a área correta da figura plana.
Figura 3: Aplicação Pick’s Theorem
Fonte: Francisco Silverio da Silva Junior
Essas atividades com a fórmula de Pick, o Geoplano e o Geogebra foram realizadas ao longo de duas aulas, nas quais pudemos notar o engajamento dos alunos na realização das atividades e a surpresa deles com a praticidade e a exatidão da fórmula de Pick.
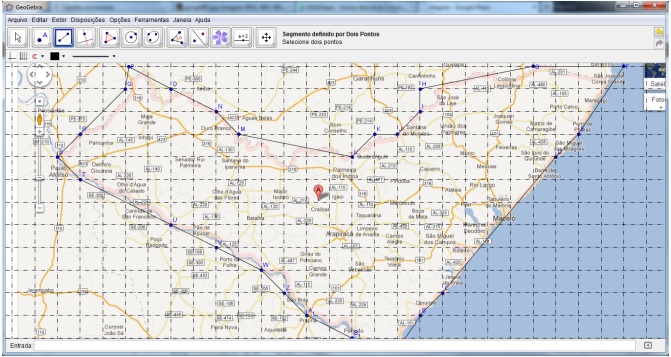
Esse interesse foi ainda maior nas duas últimas aulas do projeto, quando, depois de uma rápida revisão sobre escalas e regras de três, levamos os grupos ao laboratório de informática e os orientamos a copiar o mapa de Alagoas, retirado do Google Maps, colar no Geogebra, diagonalizar o mapa através de um polígono que contornasse a região do mapa e, com a utilização do Teorema de Pick e da escala da figura, calcular aproximações para a área do Estado. Um dos alunos conseguiu um cálculo cujo erro foi menor que 1 %. É importante mencionar que apesar de termos escolhido o Estado de Alagoas para a realização da atividade, pode-se realizar a atividade com mapas de quaisquer regiões do Google Maps.
Figura 4: Imagem do mapa de Alagoas no Geogebra
Fonte: Francisco Silverio da Silva Junior
Ao final, realizamos outro teste,[4] similar ao primeiro, com o objetivo de verificar o entendimento dos conceitos geométricos abordados durante o projeto.
Nesse teste, verificamos que todos os alunos alcançaram notas maiores ou iguais a seis pontos, dentre os quais, cinquenta por cento conseguiram notas iguais ou superiores a oito pontos, o que nos indica um avanço na assimilação dos conceitos de área e perímetro de polígonos quando comparamos aos resultados apresentados no teste inicial.
OBSTÁCULOS E CONSIDERAÇÕES FINAIS
O projeto teve início com alunos de várias turmas de primeiro ano do nível médio do nosso campus, vindos, em sua maioria, de escolas públicas e com grandes carências e dificuldades advindas de todas as limitações tão recorrentes no ensino público no Brasil. Boa parte dessas dificuldades se mostrou ao longo das aulas quando foram revisitados os conceitos de área e perímetro de figuras planas, incluindo dificuldades aritméticas nas quatro operações ou em soma de números inteiros com fração. Tudo isso nos levou a utilizar um tempo adicional para revisar essas operações e tentar sanar tais dificuldades.
Outros entraves durante o projeto foram as ocupações e greves que ocorreram no campus no final do ano de 2016, apesar de acreditarmos serem movimentos legítimos e necessários no cenário político da época. Durante as ocupações e greves, a turma se desfez e o grupo de alunos se dissipou, o que nos obrigou a realizar novo convite à comunidade discente, formando uma nova turma com quarenta alunos do segundo ano do Ensino Médio, em sua maioria. Dessa forma, reaplicamos os testes iniciais de Geometria e demos reinício às aulas práticas, que ocorreram ao longo de dez semanas.
Apesar de não termos tido tempo de testar esta sequência didática sobre o cálculo de área e perímetro em outras turmas, com os avanços conquistados apresentados nos testes e assimilação dos conceitos por parte dos alunos acreditamos que tal abordagem poderá ser um importante auxílio, não somente em nossas práticas, mas de outros professores, para combater a evasão e repetência de alunos que apresentam grandes deficiências em suas formações escolares — especialmente em matemática e em geometria — e que se sentem desmotivados para continuarem seus estudos. Pensando na divulgação de nossa experiência, por fim, decidimos reunir as sequências didáticas e sugestões de ensino dos conteúdos de Geometria com o Teorema de Pick, o Geoplano, o Geogebra e o Google Maps, numa apostila que ficará à disposição dos professores de Matemática,[5] e esperamos que esse material auxilie os professores em seus planejamentos de aula e em suas práticas docentes.
REFERÊNCIAS BIBLIOGRÁFICAS
BRASIL. Parâmetros Curriculares Nacionais: Matemática. Ministério da Educação. Secretaria de Educação Fundamental. Brasília, 1997. pp. 81-82.
PAVANELLO, Regina. M, O Abandono do Ensino da Geometria no Brasil: Causas e Consequências. Zetetiké, Campinas, n. 1, pp. 07-17, mar. 1993.
SILVA JÚNIOR, F. S. Sobre o cálculo de áreas e o teorema de Pick. 2014. 119 fls. Dissertação (Mestrado em Matemática em Rede Nacional – PROFMAT). Instituto de Matemática, Universidade Federal de Alagoas, Maceió, 2013.
[1] Disponível em: <https://1drv.ms/b/s!AmWvFxGms88Aql4qT3FQvJB16PZp>. Acesso em 10 de julho de 2018
[2] Disponível em: <https://www.geogebra.org>. Acesso em: 05 de junho de 2018
[3] Disponível em: <https://www.geogebra.org/dochopatsbu>. Acesso em: 05 de junho de 2018
[4] Disponível em: <https://1drv.ms/b/s!AmWvFxGms88Aql-OYPFlTjhc3RCm>. Acesso em: 15 de maio de 2018
[5] Disponível em: <https://1drv.ms/b/s!AmWvFxGms88AiTmQGteUnAFfSqUl>. Acesso em: 15 de maio de 2018