Aprendendo geometria analítica com o GPS

Nossas preocupações, no sentido de construção de uma sequência didática para o ensino de geometria com o uso do GPS, nos levaram a uma pesquisa teórica e prática, cujos resultados aqui, apresentamos. Fizemos uma busca de trabalhos e teorias vinculadas ao tema e ao uso de tecnologias no ensino, para considerar suas vantagens e dificuldades. Elaboramos uma sequência didática inicial e a desenvolvemos em uma turma de primeiro ano de ensino médio, com a concordância da professora e dos Estudantes, em uma Escola Estadual.^[1] Após a experiência, que consideramos positiva, reelaboramos algumas partes da sequência e a apresentamos como produção a todos os professores da escola básica.^[2]

O estudo da geometria analítica^[3] costuma, no que tange ao modelo de apresentação do conteúdo, definições, exemplos e exercícios, mostrar-se abstrato e algébrico. Pensamos em criar formas de ensino fazendo relações com a vida social e as tecnologias. Por isto pensamos no GPS,^[4] no uso do celular ou de um laboratório tecnológico, equacionando situações que estão no cotidiano social. Sistematizamos neste texto teorias que justificam propostas como essa e apresentamos um relato analítico da experiência.

O CONHECIMENTO MATEMÁTICO ESTUDADO COM O USO DO CELULAR

Palis (2010) esclarece que o conhecimento tecnológico e pedagógico do conteúdo são aqueles que os professores mobilizam para ensinar com e sobre tecnologia em suas áreas disciplinares. Nele se incluem questões instrucionais e de gestão de sala de aula, relações entre tecnologia e conteúdo específico, assim como concepções e usos pedagogicamente apropriados da tecnologia.

Borba e Penteado (2001) entendem que o uso de tecnologias no ensino de Matemática transforma a sala de aula e a própria prática do professor.        Esses autores estudam as implicações que essas novas mídias causam na prática docente, mostrando que muitos profissionais têm receio de trabalhar com a informática por medo de não superar as expectativas dos alunos ou mesmo por não terem habilidades e/ou formação para com elas lidar. Em nossas práticas observamos que os adolescentes mostram interesse em acessar tecnologias. Contudo, podemos apontar que o planejamento e prática de ensino com o uso de tecnologias demandam muito tempo, fato que hoje, infelizmente, dificulta a ação profissional, já que os docentes possuem extensa jornada de trabalho para conseguir sobreviver financeiramente. Apontamos também o aspecto relativo às condições tecnológicas que a escola deve possuir para favorecer tais ações.

Concordando com esses autores, nós entendemos que o uso de tecnologia abre possibilidades de mudanças dentro do próprio conhecimento e que é possível haver uma ressonância entre uma dada pedagogia, uma mídia e uma visão de conhecimento. Ou seja, nossa percepção da tecnologia no ensino vai ao encontro da visão de que o seu uso se articula com o conhecimento, criando uma perspectiva positiva de aprendizagem.

Moreira e David (2003; 2005) definem a matemática escolar como um conjunto de conhecimentos específicos para o ensino e que compõem a formação docente, no entendimento que conteúdos, metodologias, relações em condições da ação docente e discente não podem ser dissociados; conhecimentos são vinculados a saberes já “validados” pela docência e prática escolar. Concordamos com os autores que o conhecimento matemático-formal ganha outras formas de registro e abordagem quando está sendo ensinado, como um conhecimento tratado na formação. Desse modo, quando a matemática está sendo apresentada e aprendida pelo aluno (criança, adolescente, jovem ou adulto), pode ter linguagem mais natural, conforme o contexto e o ano em que se encontra o aluno; se mostra flexível e informal nos anos iniciais da escola básica para ir se organizando e formalizando ao longo dos anos; pode ainda ser um conhecimento abordado inicialmente de modo superficial, a partir de um fato, de um fenômeno, de solução de um problema, para ir amadurecendo os entendimentos e análises ao longo dos anos; podem também ser utilizadas justificativas livres e não apenas demonstrações^[5] com ideias intuitivas e socialmente colocadas para se ampliar para uma análise mais complexa, organizada e formal; o erro do aluno é parte do seu processo de aprendizagem e precisa ser compreendido, utilizado para se traçar novas estratégias de ensino, e não penalizado.

Em outro estudo, Ball, Thames e Phelps (2008) utilizam o termo conhecimento matemático para o ensino, reconhecendo especificidades na matéria que o professor de Matemática precisa saber para atuar na escola básica. Nessa visão, também não se pode caracterizar o conhecimento matemático estudado no ensino fundamental e médio como o conhecimento acadêmico-formal, pois se trata da abordagem passo a passo de conceitos fundamentais, base da disciplina.

As novas gerações dos adolescentes vivem uma escola onde as diferenciações cultural e social estão intrinsecamente presentes, de modo que não há que se falar em um ensino que seja por absorção de conteúdos, deixando de fora os que não seguem a proposta. A “escola para todos” é uma realidade e o ensino de Matemática precisa se apresentar de modo mais compreensivo e cumprir um papel na formação das pessoas, de modo que a matemática possa ser utilizada como instrumento de compreensão do mundo, de resolução de problemas e de preparação das pessoas de modo geral. Os velhos dispositivos que regulavam a relação professor-aluno e a relação com o conhecimento, que garantiam a autoridade pedagógica e produziam uma ordem institucional, se corroem quando deixam de ser eficientes e significativos na vida dos atores envolvidos (FANFANI, 2016). Nessa perspectiva, nosso trabalho também se alinha à pesquisa em educação matemática.

Todas essas mudanças norteiam também a forma de trabalho do professor. É necessário, às vezes, sairmos de nossa “zona de conforto” e olharmos os nossos alunos como sujeitos de aprendizagem, ou seja, pessoas ativas que têm uma história, uma memória, uma cultura. Nem sempre é possível produzir aulas diferenciadas relacionadas com mídias ou não, mas se elaborarmos uma aula pensando nesses sujeitos, talvez essa aula seja validada para esses alunos e desperte mais interesse. Nossos alunos são carentes de significados para aprender Matemática, que se mostra difícil e provoca muitos conflitos; diversificar metodologias com uso de mídias, mesmo com vários empecilhos, pode ser um meio de indicar caminhos que venham a acender uma luz, talvez com isso os próprios estudantes comecem a fazer Matemática.

ELABORAÇÃO E DESENVOLVIMENTO DA SEQUÊNCIA DIDÁTICA

A partir desses entendimentos, elaboramos uma proposta de sequência didática em busca de um material que pudesse ser experimentado, analisado e apresentado como sugestão, com orientações que facilitem o trabalho do professor para o ensino de elemento da geometria analítica. Baseia-se em conteúdos de Geometria Analítica que podem ser relacionados ao funcionamento do GPS. As atividades organizadas têm o propósito de serem desenvolvidas em turmas de qualquer ano do Ensino Médio e o seu principal objetivo é a apresentação de uma proposta de ensino que instigue o estudante, favorecendo melhor aprendizagem do conteúdo envolvido. Claro que se espera que o professor possa alterá-la da maneira que achar conveniente para atender seus alunos na realidade em que vive. Poderá, assim, segundo nossas expectativas, mostrar um caminho para o uso de tecnologia na sala de aula, articulado a uma perspectiva do conhecimento matemático escolar, ampliando possibilidades de aprendizagem.

Após as atividades prontas e desenvolvidas, elaboramos questões para uma entrevista com a professora que nos recebeu em sua sala de aula, focando em suas opiniões sobre a experiência. Durante e ao final da experiência, colhemos também as opiniões dos estudantes.

A escola selecionada possuía cerca de mil alunos e 45 professores, é uma escola de difícil acesso porque possui poucas linhas de ônibus e essas param distantes. Ela atende os alunos da própria região e de algumas regiões vizinhas, sendo que os últimos se locomovem por transporte especial. É uma região muito erma, onde os movimentos maiores são nos horários de entrada e saída da escola. A escola funciona em três turnos (manhã, tarde e noite), sendo que no período da manhã são 10 turmas (5 turmas de 2.º ano e 5 turmas de 3.º ano do Ensino Médio), no período da tarde são 10 turmas (todas de 1º ano do Ensino Médio) e no período da noite são 5 turmas (3 turmas de EJA e 2 turmas de Magistério).

Optamos por trabalhar com a única professora efetiva que estava presente à época, tendo essa mesma professora apresentado disposição em se aproximar da pesquisa. Após a leitura da atividade proposta, a professora expressou insegurança em desenvolvê-la. Refletindo sobre a situação, entendemos sua posição e tomamos a decisão de ser a própria pesquisadora a coordenar o desenvolvimento da proposta, contando com a professora para acompanhar, observar e conosco conversar sobre a experiência, o que foi muito importante. Selecionamos uma turma de primeiro ano de Ensino Médio e iniciamos as atividades.

No dia e hora combinado, chegamos à turma com as atividades impressas, incluindo orientações metodológicas específicas para a professora e folhas de exercícios dirigidos aos alunos. As folhas com as atividades impressas e respondidas pelos alunos foram recolhidas e guardadas para consulta e comprovante da pesquisa de campo.^[6] Utilizamos um caderno de campo, a gravação em áudio das atividades em sala de aula como um item importante nas etapas de levantamento de dados e análise das aulas. Seguem relatos da experiência:

A pesquisadora iniciou a aula com sua apresentação e apresentação do projeto de pesquisa, bem como das atividades que desenvolveria. Foi mencionado o uso de gravador em áudio nas aulas, nesse momento os estudantes entraram em estado de euforia, pois não são acostumados a vivenciar este tipo de situação.

Foi solicitado aos estudantes que formassem duplas e apresentado o uso do celular como item necessário ao desenvolvimento do estudo; os alunos ficaram mais uma vez eufóricos, pois este item nem sempre é permitido, mostrando grande curiosidade a respeito de como seria o uso dessa tecnologia.

As atividades da sequência didática eram em número de quinze, desenvolvidas em cinco aulas de cinquenta minutos. Inicialmente é apresentada uma situação onde claramente irá indicar a possibilidade de uso do GPS:

“Helena e suas amigas desejam conhecer uma lanchonete muito famosa que é especialista em creme de açaí. Nesta semana, seu grupo de amigas decidiu experimentar o açaí, mas elas estão com um pequeno problema, conhecem o endereço da lanchonete, mas não sabem chegar até o local. Como podemos ajudar este grupo de amigas, de um modo mais fácil, a encontrar a lanchonete? Faça no caderno um roteiro geral para se chegar à Lanchonete, saindo da Escola [apresenta-se o endereço de uma lanchonete do bairro]”.

Foi dado um tempo para que os estudantes resolvessem a questão, o que foi feito de modo bastante natural e ocorreu durante mais ou menos dez minutos; logo após esse período, a pesquisadora escutou a estratégia de cada dupla; várias respostas foram apresentadas: redação do trajeto feito a pé e do trajeto feito de ônibus, desenho de mapa para chegarem à lanchonete; alguns não conseguiram redigir e se expressaram com palavras a sua solução e outros tiveram dificuldades até na expressão com palavras e utilizaram a linguagem corporal levantando da cadeira e com movimentos braçais indicando o caminho. Surgiu também a utilização do próprio GPS, utilizando o celular, uma dupla acessou o aplicativo e foi narrando a trajetória escolhida.

Na segunda aula, foi proposto que as duplas de estudantes elaborassem um texto sobre o que entendiam do GPS; socializa-se e discute-se em seguida. Feito isso, entra um vídeo sugerido na atividade, há muita atenção e interesse, pois ele apresenta o GPS na linguagem de fácil entendimento dos adolescentes. O apresentador é um detetive com idade próxima a dos estudantes.

Na terceira aula, foram retomados ideias e comentários sobre o vídeo e o uso do dispositivo, mostrando a matemática existente no seu funcionamento. Os alunos se mostraram participativos e desejosos de conhecer o assunto. Propusemos uma atividade sobre localização, com definição de latitude e longitude, considerando o globo terrestre, eram pedidos cálculos de distância e para isto foi necessário o uso da internet. É apresentado um mapa plano do planeta, o Meridiano de Greennwich, a linha do Equador, propondo o cálculo de coordenadas. No final da aula fizemos uma rodada de correções com a participação das duplas no quadro e discutindo possíveis notações.

Na quarta aula foi apresentada uma planta baixa da própria escola e proposta atividades de marcação de pontos, deslocamento e medida de distâncias, considerando os padrões reais.  Em seguida, desenvolve-se a seguinte atividade:

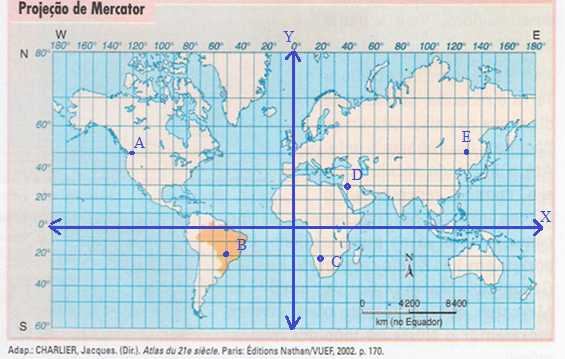
A Projeção de Mercator foi criada em 1569 pelo cartógrafo holandês Gerard Mercator. É uma projeção cartográfica cilíndrica e tornou-se a preferida dos navegantes por ser a única em que as direções podiam ser desenhadas em linha reta sobre o mapa, ou seja, apresenta uma projeção da Terra no plano. Na Projeção de Mercator, paralelos e meridianos são representados por linhas retas que se cruzam formando ângulos de 90º.

Considerando o Meridiano de Greenwich o eixo e a linha do Equador o eixo , dê as coordenadas geográficas e cartesianas das seguintes cidades A,B,C, D e E:

Os alunos se mostraram bastante interessados e desafiados e rapidamente realizaram os desafios propostos, criando estratégias para a sua resolução.

Na quinta aula, utilizando o celular, em base quadriculada, foram apresentados gráficos de coordenadas cartesianas representando o mar e nele situando barcos, propondo sua localização e cálculo de distâncias. As estratégias dos alunos podem ser assim descritas: consideraram como uma unidade cada quadrículo; para sair de um barco e chegar ao outro, percorreram os quadrículos que os separavam cortando-os, indicando a menor distância (formando a hipotenusa de um triângulo retângulo criado pelos próprios discentes); a segunda estratégia foi fazer um caminho entre os dois barcos que não era a menor distância, mas considerando cada quadrículo por inteiro (formando os catetos do triângulo retângulo). Como não foi explicitamente pedido, no enunciado do problema, que se apontasse a menor distância, as duas soluções foram aceitas. Para mostrar o cálculo da menor distância, foi possível aproveitar uma das estratégias que apareceu (a segunda), onde construímos juntos um triângulo, que os próprios alunos identificaram como triângulo retângulo. Ainda foi possível desenvolver as ideias e conhecimentos envolvendo o triângulo retângulo, por mim perguntado e por eles respondidas, de modo que aos poucos os alunos foram se familiarizando e naturalmente chegaram ao Teorema de Pitágoras, onde perceberam que o menor caminho entre os navios era a hipotenusa do triângulo retângulo. Aplicando o Teorema de Pitágoras, concluímos a fórmula de distância entre dois pontos, a partir disso ficou muito natural o aluno calcular a distância entre dois pontos quaisquer.

Na roda de conversa, ao finalizar a proposta, a quase totalidade dos alunos se expressou com poucas palavras: “Gostei.”, “Achei interessante.”, “Muito bom.”, “Saiu da mesmice da aula chata: usamos o celular” ou “Porque vimos a matemática na prática.”

APRENDENDO COM A PROPOSTA

Na experiência aqui relatada, o uso da tecnologia envolveu um instrumento de fácil acesso e disponível aos estudantes, apresentando uma série de atividades que combinavam conhecimentos de várias áreas, com correção participativa e que apresentou um conteúdo da geometria analítica de modo considerado interessante pelos próprios alunos.

Muitos foram os problemas com o uso das tecnologias que tivemos de enfrentar. Muitas vezes o acesso da escola não funcionava e tivemos de disponibilizar o do próprio celular da pesquisadora; outras vezes a sala de informática não pode ser utilizada; outras vezes havia dispersão demais, dado que o trabalho na perspectiva participativa nem sempre é o cotidiano, enfim, foram muitos os problemas vivenciados na experiência.

Acreditamos que o papel do professor está em envolver as tecnologias no aprendizado, processo esse que acontece no dia a dia, durante a prática mesmo. Outro aspecto essencial que veio da experiência foi, além da elaboração e desenvolvimento da proposta, a própria realização do relato da mesma pela pesquisadora para a elaboração da dissertação e deste texto que favorecem uma reflexão da prática, nossos entendimentos e nossa formação.

Esperamos que o relato da experiência realizada e as considerações que aqui apresentamos possam ser referência como um material didático para o trabalho do professor.

REFERÊNCIAS

BALL, Deborah Loewenberg, THAMES, Mark Hoover;PHELPS, Geoffrey.Content knowledge for teaching: what makes it special?, 2008.Disponívelem: <http://journals.sagepub.com/doi/abs/10.1177/0022487108324554?journalCode=jtea>. Acesso em: 3 de maio de 2018

BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. 4. ed., Belo Horizonte: Autêntica, 2001.

FANFANI, Emílio Tenti. Culturas jovens e cultura escolar.  Disponível em:<http://portal.mec.gov.br/seb/arquivos/pdf/CultJoEsc.pdf>. Acesso em: 3 de maio 2018

MOREIRA, Plínio C. e DAVID, Maria Manuela. Matemática escolar, matemática científica, saber docente e formação de professores. ZETETIKÉ. – Unicamp, v.11, n.19, 2003.

______.; ______. O conhecimento matemático do professor: formação e prática docente na escola básica. Rev. Bras. Educ.,n. 28, 2005. Disponível em: 10 junho 2018. Acesso em:
http://dx.doi.org/10.1590/S1413-24782005000100005.

PALIS, Gilda de La Roccque. O conhecimento tecnológico, pedagógico e do conteúdo do professor de Matemática. Educação Matemática em Pesquisa, São Paulo, v.12, n.3,2010. https://revistas.pucsp.br/index.php/emp/article/view/4288. Acesso em 10 junho 2018.

^[1] Nossa escola situa-se na cidade de Belo Horizonte, Minas Gerais, Brasil.

^[2]O trabalho completo, assim como a sequência didática, pode ser acessado no Programa de Pós-Graduação Mestrado Profissional Educação e Docência-PROMESTRE, na Faculdade de Educação da UFMG.

^[3] Chamamos de geometria analítica ao estudo de elementos matemáticos que podem ser situados no plano cartesiano, com suas relações e expressões algébricas.

^[4] GPS: global positioning sistem, ousistema de posicionamento global.

^[5] Nos referimos a demonstrações como concebida na matemática, critério rigoroso de verdade.

^[6] Professora, todos os alunos e seus pais assinaram o termo de consentimento livre e esclarecido, conforme requisitos da ética na pesquisa.